视觉残留原理:图像在人眼当中会残留1/24秒
当前动画的三大挑战:
需要与很多gameplay互动
动画是实时的,但是动画需要存储的数据量巨大
用户对真实度、流畅度的要求高
基础动画管线
创建动画,目前主要是手K和动捕
基本动画管线:
这个是比较经典的管线,现在很多图中CPU里面的计算也放在GPU里面了
2D动画技术
精灵图序列帧
Live2D(控制网格)
3D动画技术
RigidHierarchyAnimation:早期的分层级的刚体骨骼
Per-vertex Animation:顶点动画,先离线的模拟物体每一帧的顶点和法线,再每一帧实时渲染(eg.旗帜、水流)
MorphTarget:其实也是顶点动画,但是每个顶点带权重,每一帧会进行插值(eg.捏脸系统)
3D Skinned Animation(主流):蒙皮动画,其实2D骨骼也是这个技术
3D Skinned Animation
如图,蒙皮动画的原理,刷权重
不同参考系的空间
世界坐标系
模型坐标系(不是localSpace而是modelSpace)
局部坐标系(Local):每一根骨骼的坐标系
实际上的动画是在LocalSpace发生的,因为骨骼的层级关系,每一个末端骨骼的坐标都系要由上一级的骨骼累加而来,所以使用局部坐标系更方便
而局部的累计算才能得出模型坐标系,从而得出世界坐标
骨骼
Skeleton For Creature:有一般骨骼基础结构
Joint or Bone:游戏记录的树状结构是Joint,Bone是刚体,没有自由度
BindAnimation:将不同的骨骼通过Joint连接到一起,如下图,人和马共同连接了一个Joint
T-pos、A-Pos:如图,T-pos是游戏引擎表示人形骨骼的标准pos,但是由于肩颈部有挤压精度不够,渐渐被A-pos取代
3D旋转数学
欧拉角
二维:如图很好推理
三维:难点是可以绕任何轴旋转,但是数学家证明:3维空间的任何旋转都可以由三个轴的旋转叠加
即欧拉角,可以自己证明
但是欧拉角有缺点,不仅仅有顺序依赖、难以插值的问题,也有万向锁的问题
四元数
对于3维空间。
实际上分别定义了i、j、k三个虚数,即三个虚轴,
且 i*j*k = -1
具体推导不深入,最终公式
最终可以表示绕任意轴旋转
四元数的优点是易于计算,可插值、可逆计算,存储空间小,一般用于引擎内部的旋转计算
JointPose 运动数据如何记录
Orientation:关节旋转、四元数表达,使用一个3*4的矩阵,最后一列表示平移
position:位置,齐次化为3 * 4矩阵
Scale:缩放
如图:最终是一个SR的3 3矩阵表示旋转和放缩,T是一个1 3矩阵表示位移
动画一般存储在LocalSpace里面,即只存储相对于父节点的变化
为什么要存在局部坐标
如图,在模型坐标系下,插值出来的值为直线
关节与骨骼的映射关系
在关节移动时,骨骼上的Skin也需要做相应的仿射变换
上图为:每一个关节的模型坐标是由父节点的模型坐标相加而来
顶点的模型空间位置 = 关节的模型坐标 顶点相对关节的位置 = 关节的模型坐标 关节绑定模型坐标的逆 * 顶点绑定模型坐标
即:顶点绑定模型坐标 = 关节绑定模型坐标 * 顶点相对关节的位置
所以有:
即:顶点相对关节的位置(局部坐标) = 关节绑定模型坐标的逆 * 顶点绑定模型坐标,称为SkinningMatrix
所以在计算机中,关节处存储的都是绑定模型坐标的逆,如图
如何通过蒙皮权重计算蒙皮位置
其实就是一个加权平均,这个插值必须是在模型空间发生的
动画切片Clips
即在动画切片里面插值
位移和Scale是直接使用线性插值,但是旋转的插值会更加复杂
NLERP
如图,旋转的插值是使用四元数进行线性插值之后,在进行一个归一化,这就是四元数表示旋转的方便之处
注意点是,如果是大于180度的角度插值,需要进行反向插值,即最短路径的插值
以上方法称为NLERP,但是这个方式有一个缺点是,插值出来每一个角度分配的时间是不均匀的,如图,中间部分更慢,越接近起始点和终点越快,动画会不自然
SLERP
针对NLERP的问题,许多3A游戏有另一套插值方法,SLERP
即不使用矩阵插值,而是使用角度插值,但问题是运算量大,且当角度很小的时候插值不稳定
实践中的方法
一般会给定一个magicNumber,小于该角度使用NLERP,大于该角度使用SLERP
动画RunTime优化
动画压缩
动画的数据量其实是很庞大的,每一个Pose的关节坐标和clip里面的坐标变换
对大部分骨骼动画,数据大多是Rotation,而且许多关节是自身不移动的,所以动画首先是除开一些没有位移的放缩的数据
关键帧插值:
Catmull-Rom Spline:如图,是一种插值计算的数学方法,推导不重要
即将每一帧进行Catmull-Rom插值的结果计算出来,与正确结果作为比较,超过误差阈值就舍弃,并将下一帧作为关键帧,这样就能把原本的帧数压缩为少数关键帧
四元数中的浮点数压缩
可以使用定点数模拟,即使用区间映射将浮点数转化为定点数
而且可以根据四元数的特性,只存一个最大数,剩下的三个数可以通过计算还原
所以如图,原本四个浮点数可以只用6byte存储
压缩的问题
因为使用了许多压缩,会使动画有一些误差,但是由于骨骼坐标会向下累加,这些误差会放大传递到关节末端,称为Error Propagation
所以需要使用一些方法定量估计压缩前和压缩后的误差
可以通过调整末端骨骼进行误差补偿
高级动画技术
动画Blending
即从一个动画到另一个动画的过渡——线性插值(NLERP、SLERP)
但是为了避免两个动画的相差过大,一般要求两个动画进行Timeline Align
这里的blending例子权重是由一维变量决定的
Blend Space
当动画Blending需要多个变量控制时,即需要多维变量的混合动画
混合动画的算法:如图,根据二维上的点坐标找到临近的三个动画组成的三角形,再通过中心坐标进行插值
动画Mask
通过遮罩使不同的骨骼部位应用不同的动画
Additive Blending
即在原本的动画上再加一层相对量的数据,达到再加一层动画的效果
比如,在原本的动画上再加一层点头的效果,只增加相对量,而不是绝对量
Animation State Machine(ASM)
动画状态机:由节点和变换条件组成,节点包括动画切片和混合动画
Fade
Smooth Transition:动画1权重减少,动画2权重增加
Frozen Transition:动画1停止,动画2逐渐增加权重
Fade曲线:
分层状态机 LayerASM:使用LayerMask实现角色不同骨骼位置拥有单个动画状态机,现代多使用BlendTree
BlendTree
动画树的核心是定义控制变量,通过变量控制混合权重(比如在UE动画蓝图中获取pawn参数保存本地)
IK (Inverse Kinetics)
基础概念
反向动力学:以骨骼末端影响动作,比如脚掌贴合地形,手掌持枪
以Two Bone IK为例,只影响两根骨骼,如图:
已知两根骨骼边长和大腿骨骼根部到目的点的距离,使用勾股定理和三角函数可以计算出两根骨骼的偏移角度
并且需要规定这个三角形的朝向,因为上述解法的解空间在三维世界中是一个圆,无法确定一个唯一解
不然的话,例子中的关节可能会呈现不符合人体的形变
如何判断IK中的关节走向
连接多个关节时,每个关节都会有无数种偏移量符合解,需要找到一个符合人体的唯一解,如上述的TwoBonesIK,需要确定唯一解
首先判断是否能够到达目标点,计算骨骼最大距离和盲区
其次需要确定人体关节的活动范围限制
CCD算法(cyclicCoordinateDecent)
目标点依次连接每个关节,循环翻转
CCD也有非常多的优化方式,比如规定翻转最大角度,越到根节点角度越小,使翻转的角度尽可能的均摊到每一个骨骼
FABRIK (Forward And Backward Reaching IK)
首先连接末端骨骼与目标点,直接改变骨骼位移,然后连接下一个骨骼与末端骨骼位置做位移,递归到根骨骼,然后根骨骼又连接根位置,来回递归
如何处理多个IK
比如角色攀岩时,需要同时计算双手双脚四处IK,而这四处IK的根骨骼可能是同一个,每一个IK的计算都会对根骨骼有影响
解决方法:Jacobian Matrix(雅可比矩阵),在物理系统中会详讲
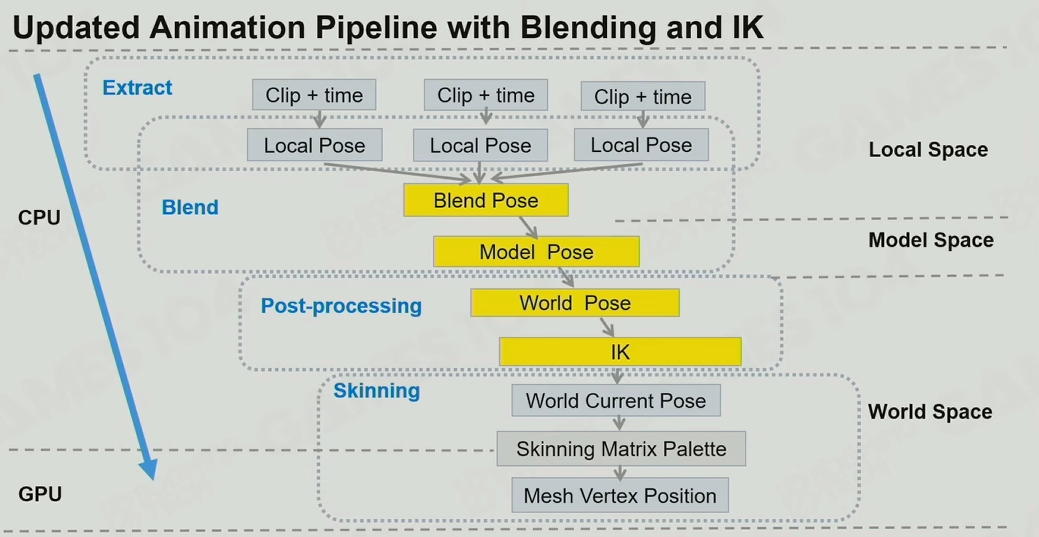
IK如何影响动画管线
如图,在一个动画管线当中加入IK之后,图中标黄的部分,先是使用混合树计算模型坐标系和世界坐标系,然后计算IK,得出新的世界坐标
表情动画
使用顶点动画MorphTarget,通过存储顶点相对于neutral表情的偏移量进行插值计算
如图:
其实除了顶点动画,也有少量的骨骼动画控制,比如眼球移动
动画重定向
动画本身记录每根骨骼相对于原始Pose的位移,所以重定向之后依旧只会根据动画的相对位移计算新的动画
不同角色骨骼的比例不同,解决位移动画问题:计算等比例位移,并且需要做一些IK
解决骨骼映射问题,会根据同名骨骼进行映射,针对同名骨骼之间多出来的骨骼会进行0-1的映射
Morph Animation重定向
对于顶点动画也是可以重定向的,因为这类动画(人物表情)也是只计算了对于neutral状态的相对偏移量。
不过依旧有一些偏差,比如眨眼动画的重定向,有些角色可能出现闭不上眼的问题,所以也有一些约束点来使动画更自然
总结
Blending系统(ASM、BlendingTree)是核心,连接gameplay系统,通过参数调整角色动画
其次使用顶点动画做人物表情,重定向技术适配不同角色骨骼

参与讨论
(Participate in the discussion)
参与讨论